URL 단축기 설계
URL 단축기 설계
요구사항
- 쓰기 연산 : 매일 1억 개의 URL 생성
- 초당 쓰기 연산 1억(100million) / 24 / 3600 = 1160
- 읽기 연산 : 읽기 연산과 쓰기 연산 비율은 10:1 이라고 하자. 그 경우 읽기 연산은 초당 11,600회 발생한다. (1160 x 10 = 11,600)
- URL 단축 서비스를 10년간 운영한다고 가정하면 1억 x 365 x 10 = 3650억 개의 레코드를 보관해야 한다.
- 축약 전 URL의 평균 길이는 100이라고 하자.
- 따라서 10년 동안 필요한 저장 용량은 3650억 x 100바이트 = 36.5TB이다.
API 엔드포인트 설계
클라이언트는 서버가 제공하는 API 엔드포인트를 통해 서버와 통신한다.
이 엔드포인트를 REST 스타일로 설계 해보자.
URL 단축기는 기본적으로 두 개의 엔드포인트를 필요로 한다.
-
URL 단축용 엔드포인트 : 새 단축 URL을 생성하고자 하는 클라이언트는 이 엔드포인트에 단축할 URL을 인자로 실어서 POST 요청을 보내야 한다. 이 엔드포인트는 다음과 같은 형태를 띤다.
POST /api/v1/data/shorten
- 인자 : {longUrl: longURLstring}
- 반환: 단축 URL
-
URL 리다이렉션용 엔드포인트 : 단축 URL에 대해서 HTTP 요청이 오면 원래 URL로 보내주기 위한 용도의 엔드포인트로, 다음과 같은 형태를 띤다.
GET /api/v1/shortUrl
- 반환 : HTTP 리다이렉션 목적지가 될 원래 URL
URL 리다이렉션
다음의 그림은 브라우저에 단축 URL을 입력하면 무슨 일이 생기는지 보여준다.
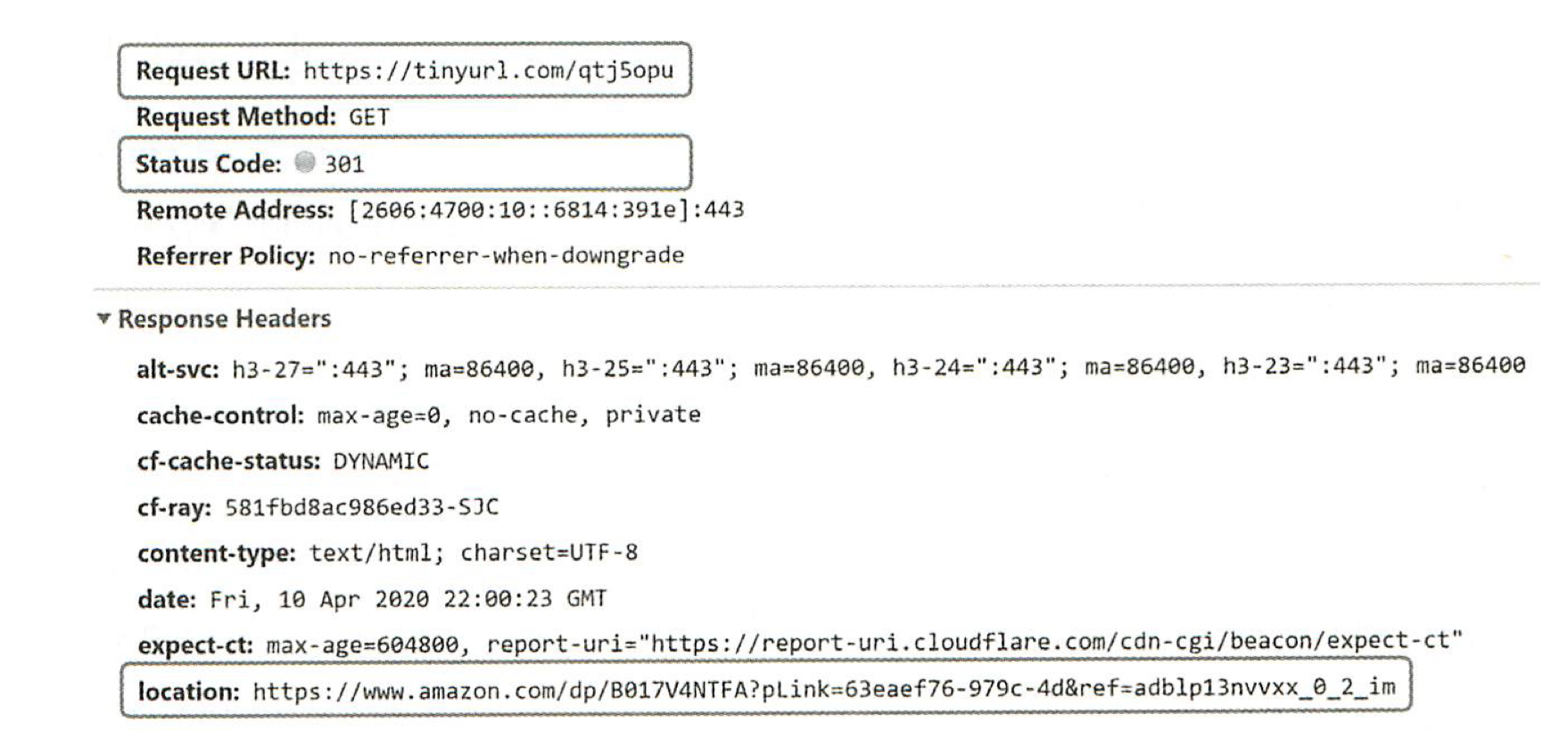
단축 URL을 받은 서버는 그 URL을 원래 URL로 바꾸어서 301 응답의 Location 헤더에 넣어 반환한다.
다음의 그림은 클라이언트와 서버 사이의 통신 절차를 좀 더 자세히 보여준다.
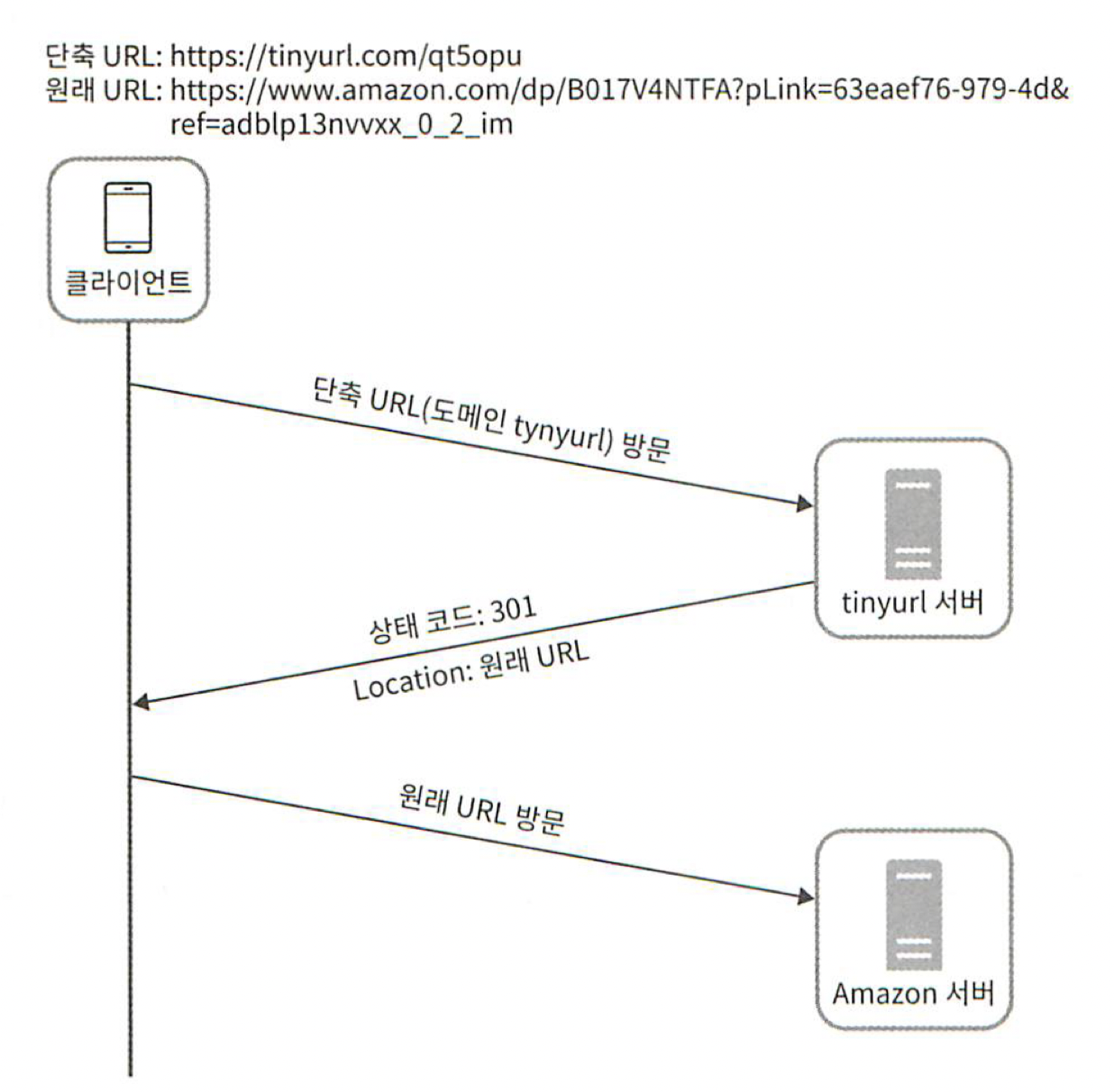
301 응답 VS 302 응답
301 응답과 302 응답 둘다 리다이렉션 응답이지만, 차이가 있다.
301 Permanetly Moved
이 응답은 해당 URL에 대한 HTTP 요청의 처리 책임이 영구적으로 Location 헤더에 반환된 URL로 이전되었다는 응답이다.
영구적으로 이전되었으므로, 브라우저는 이 응답을 캐시한다.
따라서 추후 같은 단축 URL에 요청을 보낼 필요가 있을 때 브라우저는 캐시된 원래 URL로 요청을 보내게 된다.
302 Found
이 응답은 주어진 URL로의 요청이 일시적으로 Location 헤더가 지정하는 URL에 의해 처리되어야 한다는 응답이다.
따라서 클라이언트의 요청은 언제나 단축 URL 서버에 먼저 보내진 후에 원래 URL로 리다이렉션 되어야 한다.
이 두 방법은 각기 다른 장단점을 갖고 있다.
서버 부하를 줄이는 것이 중요하다면 301 Permanent Moved를 사용하는 것이 좋은데 첫 번째 요청만 단축 URL 서버로 전송될 것이기 때문이다.
하지만 트래픽 분석이 중요할 때는 302 Found를 쓰는 쪽이 클릭 발생률이나 발생 위치를 추적하는 데 좀 더 유리할 것이다.
URL 리다이렉션을 구현하는 가장 직관적인 방법은 해시 테이블을 사용하는 것이다.
해시 테이블에 <단축 URL, 원래 URL>의 쌍을 저장한다고 가정한다면, URL 리다이렉션은 다음과 같이 구현될 수 있을 것이다.
- 원래 URL = hashTable.get(단축 URL)
- 301 또는 302 응답 Location 헤더에 원래 URL을 넣은 후 전송
URL 단축
단축 URL이 www.tinyurl.com/{hashValue} 같은 형태라고 해 보자.
결국 중요한 것은 긴 URL을 이 해시 값으로 대응시킬 해시 함수 fx를 찾는 일이 될 것이다.
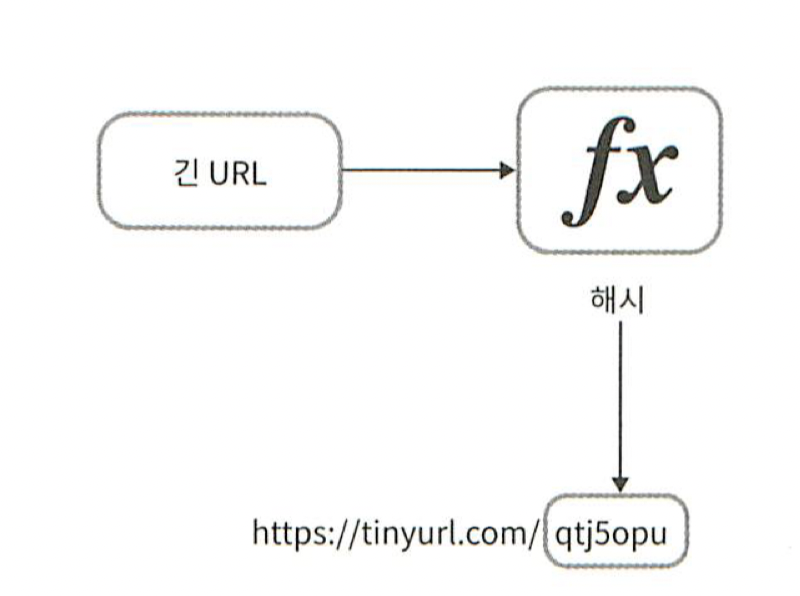
이 해시 함수는 다음 요구 사항을 만족해야 한다.
- 입력으로 주어진 긴 URL이 다른 값이면 해시 값도 달라야 한다.
- 계산된 해시 값은 원래 입력으로 주어졌던 긴 URL로 복원될 수 있어야 한다.
데이터 모델
위에서 언급했듯이 모든 것을 해시 테이블에 두었었다. 이 접근법은 초기 전략으로는 괜찮지만 실제 시스템에 쓰기에는 곤란한데, 메모리는 유한한 데다 비싸기 때문이다.
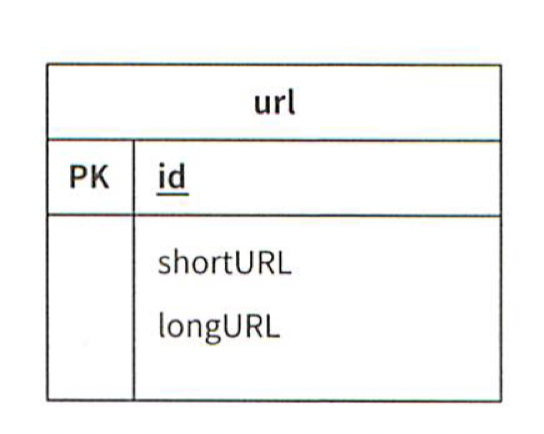
더 나은 방법은 <단축 URL, 원래 URL>의 순서쌍을 관계형 데이터베이스에 저장한느 것이다.
아래 그림이 테이블의 간단한 설계 사례다.
이 테이블은 단순화된 것으로 id, shortUrl, longURL의 세 개 컬럼을 갖는다.
해시 함수
해시 함수는 원래 URL을 단축 URL로 변환하는 데 쓰인다. 편의상 해시 함수가 계산하는 단축 URL 값을 hashValue라고 지칭하자.
해시 값 길이
hashValue는 [0-9, a-z, A-Z]의 문자들로 구성된다. 따라서 사용할 수 있는 문자의 개수는 10 + 26 + 26 = 62개다.
hashValue의 길이를 정하기 위해서는 3650억인 n의 최솟값을 찾아야 한다.
이전 요구사항에서 계산했던 추정치에 따르면 이 시스템은 3650억 개의 URL을 만들어 낼 수 있어야 한다.
다음의 표는 hashValue의 길이와, 해시 함수가 만들 수 있는 URL의 개수 사이의 관계를 나타낸다.
| n | URL 개수 |
|---|---|
| 1 | 621 = 62 |
| 2 | 622 = 3,844 |
| 3 | 623 = 238,328 |
| 4 | 624 = 14,776,336 |
| 5 | 625 = 916,132,832 |
| 6 | 626 = 56,800,235,584 |
| 7 | 627 = 3,521,614,606,208 |
| 8 | 628 = 218,340,105,584,896 |
n = 7 이면 3.5조 개의 URL을 만들 수 있다. 그러면 3650억개를 만들 수 있는 요구사항을 만족시키기 충분한 값이다.
따라서 hashValue의 길이는 7로 하면 된다.
해시 함수 구현에 쓰일 기술로는 두 가지 방법을 살펴보자.
하나는 해시 후 충돌 해소 방법이고, 다른 하나는 base-62 변환 법이다.
해시 후 충돌 해소
긴 URL을 줄이려면, 원래 URL을 7글자 문자열로 줄이는 해시 함수가 필요하다.
손쉬운 방법은 CRC32, MD5, SHA-1같이 잘 알려진 해시 함수를 이용하는 것이다.
아래는 해시 함수를 사용하여 https://en.wikipedia.org/wiki/Systems_design 을 축약한 결과다.
| 해시 함수 | 해시 결과 (16진수) |
|---|---|
| CRC32 | 5cb54054 |
| MD5 | 5a62509a84df9ee03fe1230b9dfb84e |
| SHA-1 | 0eeae7916c06853901d9ccbefbfcaf4de57ed85b |
그런데 위의 표와 같이, CRC32가 계산한 가장 짧은 해시값조차도 7보다는 길다.
어떻게 하면 줄일 수 있을까?
이 문제를 해결할 첫 번째 방법은 계산된 해시 값에서 처음 7개 글자만 이용한느 것이다.
하지만 이렇게 하면 해시 결과가 서로 충돌할 확률이 높아진다.
충돌이 실제로 발생했을 때는, 충돌이 해소될 때까지 사전에 정한 문자열을 해시값에 덧붙인다.
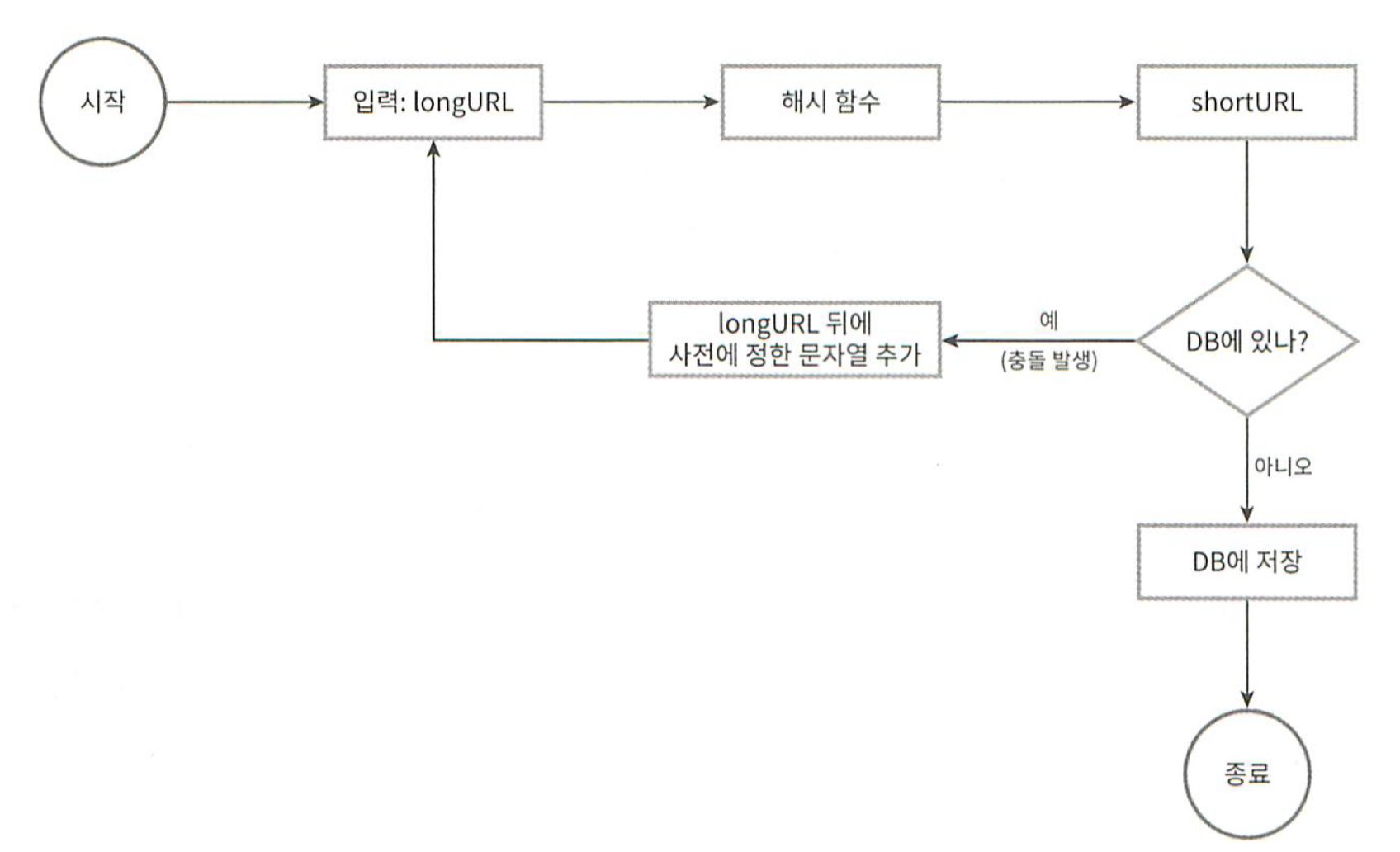
이 방법을 쓰면 충돌은 해소할 수 있지만 단축 URL을 생성할 때 한 번 이상 데이터베이스 질의를 해야하므로 오버헤드가 크다.
데이터베이스 대신 블룸 필터를 사용하면 성능을 높일 수 있다.
base-62 변환
진법 변환은 URL 단축기를 구현할 때 흔히 사용되는 접근법 중 하나다.
이 기법은 수의 표현 방식이 다른 두 시스템이 같은 수를 공유하여야 하는 경우에 유용하다.
62진법을 쓰는 이유는 hashValue에 사용할 수 있는 문자 개수가 62개이기 때문이다.
1115710을 62진수로 변환해보자.
- 62진법은 수를 표현하기 위해 62개의 문자를 사용하는 진법이다. 따라서 0은 0으로 9는 9로, 10은 a로 61은 Z로 대응시켜 표현하도록 할 것이다. 따라서 62진법에서 ‘a’는 10을 나타내고 ‘Z’는 61을 나타낸다.
- 1115710 = 2 x 622 + 55 X 621 + 59 x 620 = [2, 55, 59] => [2, T, X] => 2TX62 이다.
- 따라서 단축 URL은 https://tinyurl.com/2TX가 된다.
두 접근법 비교
| 해시 후 충돌 해소 전략 | base-62 변환 |
|---|---|
| 단축 URL의 길이가 고정됨 | 단축 URL의 길이가 가변적. ID 값이 커지면 같이 길어짐 |
| 유일성이 보장되는 ID 생성기가 필요치 않음 | 유일성 보장 ID 생성기가 필요 |
| 충돌이 가능해서 해소 전략이 필요 | ID 유일성이 보장된 보장된 후에야 적용 가능한 전략이라 충돌은 아예 불가능 |
| ID로부터 단축 URL을 계산하는 방식이 아니라서 다음에 쓸 수 있는 URL을 알아내는 것이 불가능 | ID가 1씩 증가하는 값이라고 가정하면 다음에 쓸 수 있는 단축 URL이 무엇인지 쉽게 알아낼 수 있어서 보안상 문제가 될 소지가 있음 |
